SOLUTION
Given the question in the image, the following are the solution steps to answer the question.
STEP 1: Write the first two vertices given
STEP 2: Find the slope
The side connecting the two given points will be gotten using distance formula;
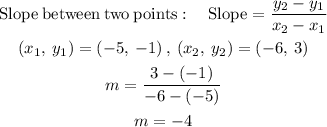
Slope is -4
STEP 3: Write the second two vertices given
STEP 4: find the slope
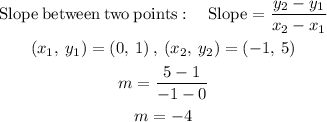
Slope is -4