The Pythagorean Theorem states that:
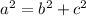
Where "a" is the hypotenuse of the Right triangle and "b" and "c" are the legs.
The hypotenuse is the longest side of the triangle.
You can apply the Pythagorean Theorem in each option given in the exercise, in order to identify which side lengths form a Right triangle:
A) Knowing that:
![\begin{gathered} \sqrt[]{9}=3 \\ \sqrt[]{18}\approx4.24 \end{gathered}](https://img.qammunity.org/qa-images/2023/formulas/mathematics/college/xybmyk5awdeu0j7c6oo7.png)
You can identify that, if it is a Right triangle, the hypotenuse would be
![a=\sqrt[]{18}](https://img.qammunity.org/qa-images/2023/formulas/mathematics/college/usufm0qrob3l3bcxw2p9.png)
Then, applying the Pythagorean Theorem, you get:
![\begin{gathered} (\sqrt[]{18})^2=(\sqrt[]{9})^2+3^2 \\ 18=9+9 \\ 18=18 \end{gathered}](https://img.qammunity.org/qa-images/2023/formulas/mathematics/college/vuweg9h9p360717wuec7.png)
Therefore, these sides lengths form a Right triangle.
B) The hypotenuse would be:
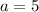
Applying the Pythagorean Theorem:
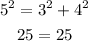
These sides lengths form a Right triangle.
C) Since:
![\sqrt[]{98}\approx9.9](https://img.qammunity.org/qa-images/2023/formulas/mathematics/college/88iuwz1qed983cdc995c.png)
That would be the hypotenuse. Therefore, applying the Pythagorean Theorem, you get:
![\begin{gathered} (\sqrt[]{98})^2=7^2+7^2 \\ 98=98 \end{gathered}](https://img.qammunity.org/qa-images/2023/formulas/mathematics/college/g56fmwp7mcarx5jy1y8y.png)
These sides lengths form a Right triangle.
Therefore, the answer is: Options A, B and C.