Question

Determine tan(t) if cos(t)= -3/5 and sin(t) >0

Answer 1

`\bf cos(\theta)=\cfrac{adjacent}{hypotenuse} \qquad % tangent tan(\theta)=\cfrac{opposite}{adjacent}\\\\ -------------------------------\\\\ cos(t)=-\cfrac{\stackrel{adjacent}{3}}{\stackrel{hypotenuse}{5}}`

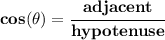
now, the hypotenuse is just a radius unit, so, is never negative, so, the fraction is negative because the numerator is negative, that is, the adjacent side is -3.

now, let's use the pythagorean theorem to find the opposite side.


`\bf \textit{using the pythagorean theorem}\\\\ c^2=a^2+b^2\implies \pm√(c^2-a^2)=b\qquad \begin{cases} c=hypotenuse\\ a=adjacent\\ b=opposite\\ \end{cases} \\\\\\ \pm√(5^2-(-3)^2)=b\implies \pm√(25-9)=b\implies \pm 4=b`

ok... so, which is it? the +/-? well, we also know that sin(t) >0, namely that the sine of the angle is positive, so, then is +4 then.


`\bf tan(\theta)=\cfrac{opposite}{adjacent}\qquad \qquad tan(t)=\cfrac{4}{-3}\implies \boxed{tan(t)=-\cfrac{4}{3}}`