Question

A convex polyhedron has (8a) faces, (6a + 6) vertices, and (15a) edges. What is the value of a?

Euler’s formula: V + F = E + 2

a =

Answer 1

6a+6+8a=15a+2
a=4
So there are 32 faces, 30 vertices, and 60 edges

Answer 2

Answer: 4

Explanation:

Given: A convex polyhedron has (8a) faces, (6a + 6) vertices, and (15a) edges.

Euler’s formula:

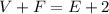`V + F = E + 2`, where V is number of vertices , F is number of faces and E is number of edges in a polygon.

Substituting the given values of V,E and F in the Euler's formula, we get

`6a+6+8a=15a+2\\\\\Righatrrow\ 14a+6=15a+2`

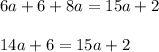
Subtract 14a and 2 on both the sides, we get

`a=6-2=4`