Question

James perkins wants to have a million dollars at retirement, which is 15 years away. he already has $200,000 in an ira earning 8 percent annually. how much does he need to save each year, beginning at the end of this year to reach his target? assume he could earn 8 percent on any investment he makes. (round to the nearest dollar.)

Answer 1

The value of a principal amount of $200,000 after 15 years, ar a rate of 8% compounded monthly, is
A = $200,000(1 + 0.08/12)⁽¹² * ¹⁵⁾ = 200000*(1.0067¹⁸⁰) = $661,384.30

If $x is deposited every year, the value of each additional investment will be
x*1.0067¹⁶⁸ = 3.0705x for 14 years
x*1.0067¹⁵⁶ = 2.8341x for 13 years
x*1.0067¹⁴⁴ = 2.6158x for 12 years
and so on

The extra deposits form a geometric sequence with
a = 3.0705x
r = 0.923

The sum of the 14 terms of the sequence is

`(a(1-r^(14)))/(1-r) = (3.0705x(1-0.923^(14)))/(1-0.923) =26.8886x`

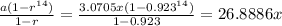
The total investment is worth $1,000,000 after 15 years. Therefore
661,384.30 + 26.8886x = 1,000,000
26.8886x = 338,615.70
x = $12,593.28

Answer:
James saves $12,593.28 each year.