Question

List the possible zeros of the polynomial:

2x^3+5x^2-31x-15

Answer 1

The zeros are approximately x = -5.25, -0.5, and 3.1.

Answer 2

We want to list the possible zeros of
f(x) = 2x³ + 5x² - 31x - 15
There are 3 possible zeros because the polynomial is of degree 3.

There is one change in sign, so there is one real positive zero according to Descartes' Rule of Signs
f(-x) = -2x³ + 5x² + 31x - 15
There are two changes in sign, so there are 2 real negative zeros.

According to the Rational Zeros Theorem, if f(a) = 0, then x=a is a zero of f(x).
A graph of f(x) reveals that there are indeed three real zeros (one positive, two negative) as expected, but no integral zeros of f(x) exist.

Answer:
The zeros are approximately x = -5.25, -0.5, and 3.1.

Note (If you know calculus):
The zeros are in the vicinity of x = -5.25, -0.5, 3.1.
To estimate them accurately, we can use the Newton-Raphson formula. That is,

`x_(n+1) = x_(n) - (f(x_(n)))/(f'(x_(n))) , \, n=0,1,2, \, ..., \\ where \\ f'(x) = 6x^(2) + 10x - 31`
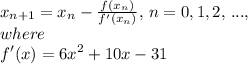
For each zero, set x₀ = -5.25, -0.5, 3.1 for the teratons.
Results:
1st zero:
n=0, x= -5.2277
n=1, x= -5.2025
n=2, x= -5.2023
n=3, x= -5.2023 (converged)
2nd zero:
n=0, x= -0.4565
n=1, x= -0.4564
n=2, x= -0.4564 (converged)
3rd zero:
n=0, x= 3.1601
n=1, x= 3.1587
n=2, x= 3.1587 (converged)

The zeros are -5.2023, -0.4564, and 3.1587.