Question

An arithmetic sequence with a third term of 8 and a constant difference of 5.

Answer 1

An arithmetic sequence (a_n) is as follows:


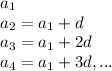
`a_1\\a_2=a_1+d\\a_3= a_1+2d\\a_4=a_1+3d,...` where
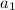
`a_1` is the first term and d is the constant difference,

thus, we see that the n'th term of an arithmetic sequence is
`a_n=a_1+(n-1)d`


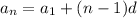
in our particular case d=5, the third term is 8, so we have:


`a_3=8=a_1+2\cdot5\\\\8=a_1+10\\\\a_1=-2`


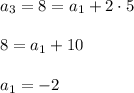
and the general term is
`a_n=-2+5(n-1)`,


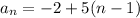
Answer: first term is -2, n'th term is -2+5(n-1)