Answer:
The standard deviation of the data is 0.7.
Explanation:
Given : Data 7.7, 8.4, 9, 8, 6.9
To find : What is the standard deviation of the following data set rounded to the nearest tenth?
Solution :
We can apply the standard deviation formula,
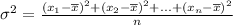
Where,
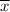 is the arithmetic mean
is the arithmetic mean
First we find the arithmetic mean
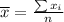
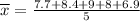
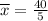
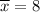
Now, substitute the values in the standard deviation formula,
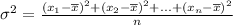
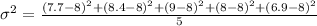
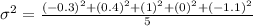
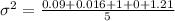
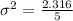
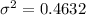
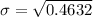
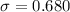
Therefore, The standard deviation of the data is 0.7.