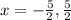Question

STEP #1. completely factor the left-hand side of the equation into two or more factors.STEP #2. solve the given equation by factoring. write your answer in reduced fraction form, if necessary.

Answer 1

The expression we have is:

`64x^4-25x^2=0`

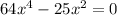
Step 1. In this step, we have to factor the left-hand side of the equation.

The first thing we will do is to simplify the expression by dividing everything by x^2:

`(64x^4)/(x^2)-(25x^2)/(x^2)=(0)/(x^2)`

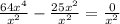
To divide the expression we use the following law of exponents:

`(x^m)/(x^n)=x^(m-n)`

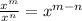
And we get the simplified expression:

`64x^2-25=0`

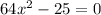
This equation is equivalent to the one given by the problem.

The second step is to represent 64 and 25 as 8 to the power of 2 and 5 to the power of 2:

`\begin{gathered} 8^2=64 \\ 5^2=25 \end{gathered}`

Substituting this in our expression:

`8^2x^2-5^2=0`

Which can also be written as follows:

`(8x)^2-(5)^2=0`

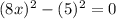
Here we can use the formula for a difference of squares:

`a^2-b^2=(a+b)(a-b)`

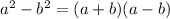
In this case a=8x and b=5, so we get the factored expression:

`(8x+5)(8x-5)=0`

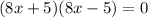
This is the solution for step 1.

Step 2. In this second step, we have to solve the factored equation we got in step 1.

First, we use the zero product property, which tells us that if a product of two expressions is equal to 0, at least one of them or the two are equal to 0. So we equal to 0 the two parts of parentheses of the factored expression:

`\begin{gathered} (8x+5)=0 \\ (8x-5)=0 \end{gathered}`

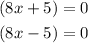
And we solve both equations to find the two solutions for the value of x.

Solving the first equation we get the first x-value:

`\begin{gathered} 8x+5=0 \\ 8x=-5 \\ x=-(5)/(8) \end{gathered}`

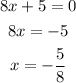
Solving the second equation we get the second x-value:

`\begin{gathered} 8x-5=0 \\ 8x=5 \\ x=(5)/(8) \end{gathered}`

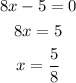
Thus, we get the two values for x:

`x=-(5)/(2),(5)/(2)`