Question

V²-12x+28=-7Need to solve each equation by completing the square for number eight

Answer 1

v=7, 5

Step-by-step explanation:

Given the equation:

`v^2-12v+28=-7`

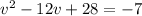
To solve for v using completing the square method, follow the steps below:

Step 1: Take the constant to the right-hand side.

`\begin{gathered} v^2-12v=-7-28 \\ \implies v^2-12v=-35 \end{gathered}`

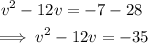
Step 2: Divide the coefficient of x by 2, square it and add it to both sides.

`v^2-12v+(-6)^2=-35+(-6)^2`

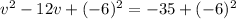
Step 3: Write the left-hand side as a perfect square.

`(v-6)^2=-35+36\implies(v-6)^2=1`

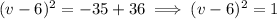
Step 4: Take the square root of both sides.

`\begin{gathered} √((v-6)^2)=\pm√(1) \\ v-6=\pm1 \end{gathered}`

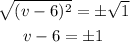
Step 5: Solve for v.

`\begin{gathered} v=6\pm1 \\ v=6+1\text{ or }v=6-1 \\ v=7\text{ or }v=5 \end{gathered}`

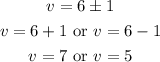
The values of v are 7 and 5.