Question

A thief plans to steal a gold sphere with the radius of 28.9cm from a museum. If the gold has a density of 19.3 g/cm^3 what is the mass of the sphere in pounds? (Volume of a sphere is V= (4/3) pi r^3) Is the thief likely to be able to walk off with gold sphere unassisted?

Answer 1

First you have to plug the radius (28.9 cm) in the equation for volume, so you would have V = (4/3)*pi*(28.9)^3(which means cubed) to get 101107.2126 cm^3 for volume, next use that in the formula m = d*V = 19.3g/cm^3 * 101107.2126 to get 1,951,369.203g to convert to pounds you multiply that by 0.00220462262 or 0.002 for short to get 4,302.03 pounds
Unless he can carry 4k pounds, I don't think he getting away.

Answer 2

Answer: The mass of gold in pounds is 4299.8 pounds.

Step-by-step explanation:

To calculate the volume of sphere, we use the formula:

`V=(4)/(3)\pi r^3`

where,

r = radius of sphere

We are given:

Radius of osmium = 28.9 cm

Volume of osmium =
`(4)/(3)* 3.14* (15)^3=101056cm^3`

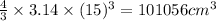
Density of gold =
`19.3g/cm^3`

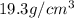
To calculate mass of a substance, we use the equation:

`Density=(Mass)/(Volume)`

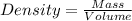
Putting values in above equation, we get:

`19.3g/cm^3=\frac{\text{Mass of gold}}{101056cm^3}\\\\\text{Mass of gold}=1950380.8g`

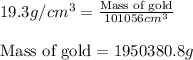
To convert the given mass into pounds, we use the conversion factors:

1 pound = 453.592 g

So,
`1950380.8g=1950380.8g* (1pound)/(453.592g)=4299.8pounds`

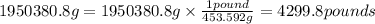
Hence, the mass of gold in pounds is 4299.8 pounds.