Question

how do I know where to place the angles in order from largest (at the top) to smallest (at the bottom)?

Answer 1

To do this, you can determine how much each angle measures using the cosine law, which is a formula that relates the angles to the sides of any triangle.

`\begin{gathered} a^2=b^2+c^2-2bc\cdot\cos (A) \\ b^2=a^2+c^2-2ac\cdot\cos (B) \\ c^2=a^2+b^2-2ab\cdot\cos (C) \end{gathered}`

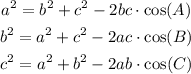
For example, to first find the measure of angle A, you have

`\begin{gathered} a=9,b=8,c=7 \\ a^2=b^2+c^2-2bc\cdot\cos (A) \\ \text{Solve for A and replace the side measurements} \\ a^2+2bc\cdot\cos (A)=b^2+c^2-2bc\cdot\cos (A)+2bc\cdot\cos (A) \\ a^2+2bc\cdot\cos (A)-a^2=b^2+c^2-a^2 \\ 2bc\cdot\cos (A)=b^2+c^2-a^2 \\ \cos (A)=(b^2+c^2-a^2)/(2bc) \\ \cos (A)=(8^2+7^2-9^2)/(2(7)(8))=(32)/(112) \\ \cos (A)=0.2857 \\ \text{ Apply to both sides of the equation }\cos ^(-1)(x)\text{ which is the inverse function of cos (x)} \\ \cos ^(-1)(\cos (A))=\cos ^(-1)(0.2857)\text{ } \\ A=73.4 \end{gathered}`

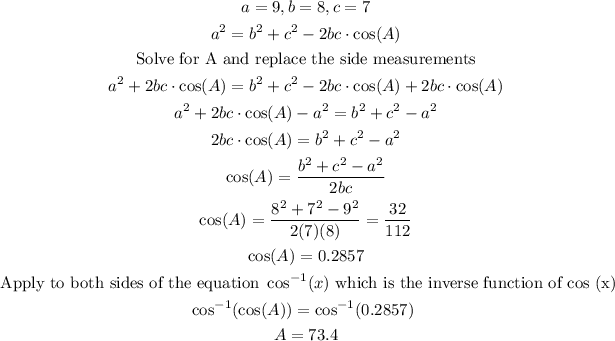
Similarly, you can find the angle B

`\begin{gathered} \cos (B)=(a^2+c^2-b^2)/(2ac) \\ \cos (B)=(9^2+7^2-8^2)/(2(9)(7))=(11)/(21) \\ \cos (B)=0.5238 \\ \cos ^(-1)(\cos (B))=\cos ^(-1)(0.5238) \\ B=58.4 \end{gathered}`

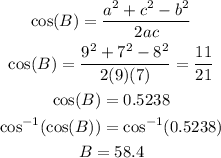
To find the angle C you can use the following expression that indicates that the sum of the internal angles of a triangle is 180

`\begin{gathered} A+B+C=180 \\ 73.4+58.4+C=180 \\ C=180-73.4-58.4 \\ C=48.2 \end{gathered}`

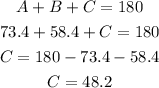
Therefore, the order of the angles from largest to smallest is