Question

Two pyramids are similar.• The surface area of the first is 250 and the surface area of the second is 22.5.The heights of the pyramids are in a ratio ofThe volumes of the pyramids are in a ratio ofBlank 1:Blank 2:Blank 3:Blank 4:

Answer 1

We are told that both prisms are similar.

This means that if we take the dimensions of one prisms, and multiply them by a constant of proportionality, we get the dimensions of the other prism.

We are given the heights of both prisms, so if we take the height of the first prism (say 2 cm) and we multiply it by a constant, we should get the height of the second. So we have the equation

`2\cdot k=5`

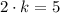
So if we divide both sides by 2, we get that the constant of proportionality is

`k=(5)/(2)`

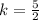
If we take the width of the first prism and multiply it by the constant of proportionality, we get

`4\cdot(5)/(2)=2\cdot5=10`

So the width of the second prism is 10cm.

Assuming that we are given rectangular prisms, we can see that the volume of the prism is simply the product of the height, the length and the width. So for the second prism we woud have the volume

`w_2\cdot h_2\cdot l_2=((5)/(2))\cdot w_1\cdot((5)/(2))\cdot h_1\cdot((5)/(2))\cdot l_1=((5)/(2))^3\cdot w_1\cdot l_1\cdot h_1=24\cdot(125)/(8)=3\cdot125=475`

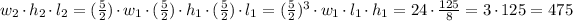
So the volume of the second prism is 475 cubic cm.