We are told that both prisms are similar.
This means that if we take the dimensions of one prisms, and multiply them by a constant of proportionality, we get the dimensions of the other prism.
We are given the heights of both prisms, so if we take the height of the first prism (say 2 cm) and we multiply it by a constant, we should get the height of the second. So we have the equation
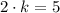
So if we divide both sides by 2, we get that the constant of proportionality is
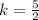
If we take the width of the first prism and multiply it by the constant of proportionality, we get
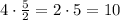
So the width of the second prism is 10cm.
Assuming that we are given rectangular prisms, we can see that the volume of the prism is simply the product of the height, the length and the width. So for the second prism we woud have the volume
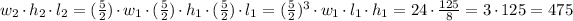
So the volume of the second prism is 475 cubic cm.