Answer: The correct option is (C)
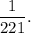
Step-by-step explanation: Given that two cards are drawn from a standard 52-card deck without replacement.
We are to find the probability that both the cards are aces.
We know that there are 4 aces in a deck of 52 cards.
Let S denote the sample space for the experiment of drawing a card from a deck of 52 cards.
Then, n(S) = 52.
Let A denote the event that the first card drawn is an ace.
Then, n(A) = 4.
So, probability of event A will be

Now, since the second card is drawn without replacing the first ace card, so the probability that both the cards are aces will be
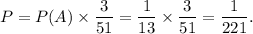
Thus, the required probability is
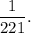
Option (C) is CORRECT.