Question

`\footnotesize \rm Find \: the \: lower \: limit \: of \: x \: in \: the \: triple \: integral \\ \footnotesize {{{ \displaystyle \rm { \iiint_D}}}} \rm f(x,y,z) \: dV \: if \: D \: is \: solid \: bounded \\ \footnotesize \rm z=4-y, z=y-6 \: and \: y=x², taking \: the \\ \footnotesize \rm the \: order \: of \: integration \: as \: dzdydx.`​

Answer 1

The integral with the prescribed order of integration would be

`\displaystyle \iiint_D f(x,y,z) \, dV = \int_(-\sqrt5)^(\sqrt5) \int_(x^2)^5 \int_(4-y)^(y-6) f(x,y,z) \, dz \, dy \, dx`

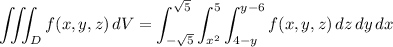
• z is bounded between two planes, z = 4 - y and z = y - 6. These planes meet in a line with coordinates y = 5 and z = -1. Deciding which plane lies above the other comes down to checking the value of z for some y-coordinate of any point that we know belongs to D. The parabolic face y = x² contains the origin (0, 0, 0), so we know there are points in D with y-coordinate = 0. When y = 0,
z = 4 - y = 4
z = y - 6 = -6
and this tells us that 4 - y is the "upper" plane.

• y is bounded between the parabolic cylinder y = x² and the plane y = 5, which we determined earlier when finding where the two planes intersect. This also tells us that 0 ≤ y ≤ 5 for any point in D.

• x is bounded between -√5 and +√5, since at most y = 5, so that
y = 5 = x² ⇒ x = ±√5