Question

Analyze the asymptotes of the function.

y=1 / x+4
Which of the following options are the equations of the function’s asymptotes? Select all that apply.
x = -4
x = 4
y = -4
y = 4
x = 0
y = 0

Answer 1

the asymptotes will be the values for x and y that cannot exist. With fractions, you can never have a zero denominator, so solving for: x+4=0
says that x cannot be -4. That line x =-4 is a vertical asymptote where the function cannot cross.

Then you look at y, rearrange the equation.
y = 1/(x+4)
y(x+4) = 1
(x+4) = 1/y

now you can see y can never be zero. The line y = 0 is a vertical asymptote that the function will never cross over, only approach.

Answer 2

Option 1 and 6.

The vertical asymptote is x=-4.

The horizontal asymptote is y=0.

Explanation:

Given : Function
`y=(1)/(x+4)`

To find : Analyze the asymptotes of the function?

Solution :

Asymptote is a line that the graph of a function approaches but never touches.

To find the vertical asymptote put the denominator equal to zero and find the value of x.

`y=(1)/(x+4)`

Denominator =0

`x+4=0`

`x=-4`

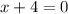
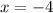
So, vertical asymptote is x=-4.

Now, to find the horizontal asymptote we see the degree of both numerator and denominator.

`y=(1)/(x+4)`

Degree of numerator is 0

Degree of Denominator = 1

We know, When the degree of numerator is less than the degree of denominator then the horizontal asymptote is y=0.

Therefore, From the given options, Option 1 and 6 is correct.

The vertical asymptote is x=-4.

The horizontal asymptote is y=0.