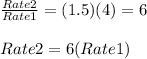Answer:
The reaction rate will increase by a factor of 6
Rate2 = 6(Rate1)
Step-by-step explanation:
The given reaction is:
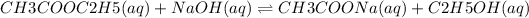
![Rate = k[CH3COOC2H5]^(m)[NaOH]^(n)](https://img.qammunity.org/2018/formulas/chemistry/high-school/pd8wxpdl3itgtt6wyh0p7y2hu076gxv56d.png)
k = rate constant
m = order w.r.t to
 = 1
= 1
n = order w.r.t to
 = 1
= 1
Therefore, the initial rate is:
![Rate1 = k[CH3COOC2H5][NaOH]](https://img.qammunity.org/2018/formulas/chemistry/high-school/gtyyl2iy0nmtxv8etuar484dwggl3x6grn.png)
It is given that
![[CH3COOC2H5]](https://img.qammunity.org/2018/formulas/chemistry/high-school/eic7s1lbxb391auk692bodgjz0ej7fqvk3.png) is increased by 1/2. Therefore the new concentration =
is increased by 1/2. Therefore the new concentration =
![[CH3COOC2H5] + (1)/(2)[CH3COOC2H5] = 1.5 [CH3COOC2H5]](https://img.qammunity.org/2018/formulas/chemistry/high-school/eyjs2q8joildgilphaou7rchvlk7l7ssac.png)
It is given that the concentration of
 was quadrupled. Similarly, new concentration of
was quadrupled. Similarly, new concentration of
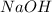 is =
is =
![4[NaOH]](https://img.qammunity.org/2018/formulas/chemistry/high-school/796iqdvz5m0aqvgkfr8h8vxg3h27sugi23.png)
Therefore, the new rate is:
![Rate2 = k[1.5CH3COOC2H5][4NaOH]](https://img.qammunity.org/2018/formulas/chemistry/high-school/b1bjguj5c3f02pkg78j07fmxlc14nh2glj.png)