We have a normal distribution for the cost with mean 27,500 and standard deviation 7,740.
a) We have to find the probability of that the cost is less than 20,000.
We have to calculate the z-value for x=20,000 and then look for the probability for the interval using the z-value in the standard normal distribution.
The z-value can be calculated as:

Then, we can look at the probability in a table or app:
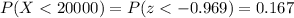
b) Now, we have to to calculate the probability of the average cost for a sample of 3 families be more than 40,000.
In this case, the standard deviation for a sampling distribution is the quotient between the standard deviation of the population and the square root of the sample size.
Then, we can calculate the z-value as:
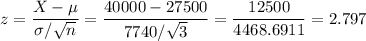
We can now calculate the probability as:

c) To calculate the probability for an interval like this, we have to calculate the z-values for the extremes of the intervals:
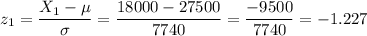
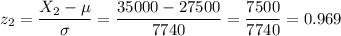
Now we can calculate the probability as:
![\begin{gathered} P(18000d) In this case, we have a sample size of n=5. We calculate the standard deviation for the sampling distribution dividing the standard deviation of the population by the square root of the sample size, and use it to calculate the z-value:[tex]z=(X-\mu)/(\sigma/√(n))=(32000-27500)/(7740/√(5))=(4500)/(3461.4332)=1.300]()
Then, we calculate the probability as:
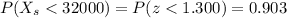
Answer:
a) P(X<20,000) = 0.167
b) P(Xs>40000) = 0.003
c) P(18000
d) P(Xs<32000) = 0.903