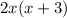Answer:
The factored expression is:
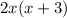
Explanation:
We are given the following expression:
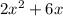
To factorize it as fully as possible, we first find the GCF between the numeric values, and the coefficients:
Numeric:
GCF between 2 and 6 is 2, because:
2 - 6| 2
1 - 3|
1 and 3 are not divisible by the same number, so 2.
Coefficient:
Between x² and x, x.
Factorizing:
Simplifying by 2x.
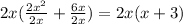
The factored expression is: