Question

Radium-223, a common isotope of radium has a half life of 11.4 days. Professor Korbel has a 120 gram sample of radium-223 in his laboratory. How long until there was only 100 grams remaining?( round to the nearest hundredth of a day )

Answer 1

1) Gathering the data

The half-life of Radium 223: 11.4 days

Initial Mass of Rd-223 : 120g

The final mass of Rd-223: 100

2) Let's use one of our possible formulas for exponential decay to calculate how long until Radium-223 gets from 120g to 100grams. And applying properties of the Logarithm

`\begin{gathered} N=N_0((1)/(2))^{\frac{t}{t\text{ 1/2}}} \\ 100=120\text{ (}(1)/(2))^{(t)/(11.4)} \\ (100)/(120)=(120)/(120)\text{(}(1)/(2))^{(t)/(11.4)} \\ (5)/(6)=((1)/(2))^{(t)/(11.4)} \\ \log _(10)(5)/(6)=\log _(10)((1)/(2))^{(t)/(11.4)} \\ -0.0792=(t)/(11.4)\log _(10)(1)/(2) \\ -0.0792=(t)/(11.4)(-0.301) \\ -0.0792=-(0.301t)/(11.4) \\ -0.90288=-0.301t \\ t=2.9996\approx\text{ 3 days} \end{gathered}`

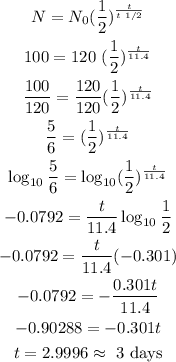
3) So it will take approximately 3 days to the Radium-223 isotope reduce to 100 grams.