Given:
Use the Factor Theorem to determine whether x + 3 is a factor of P(x)=x⁴+x³-4x² +8.
Required:
Determine if x + 3 factor or not.
Step-by-step explanation:
We know by factor theorem that if f(a) = 0 for a polynomial then (x - a) is a factor of the polynomial f(x).
It means for (x + 3) to be factor f(-3) = 0
Now,
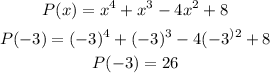
We get, P(-3) is not equal zero. So, (x + 3) is not a factor.
Answer:
x + 3 is not a factor of P(x).