Question

An object 8 cm tall is placed at different locations in front of a concave mirror whose radius of curvature is 85 cm. Determine the magnification of the image when the object distance is 20 cm.

Answer 1

1.89

Step-by-step explanation

Given:

• The height of the object, h = 8 cm

,

• The radius of curvature of the concave mirror, R = 85 cm

,

• The distance of the object, u = 20 cm

Find:

• The magnification of the image, m

First, we can find the focal length of the mirror,

`f=(R)/(2)\Rightarrow f=(85cm)/(2)=42.5cm`

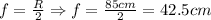
Now, using the mirror's formula, we can find the distance of the image, v. Note that the object is 20 cm away from the mirror, which means it is located between the mirror and the focal point,

So, the image will be behind the mirror (virtual image).

The mirror's formula in this case is,

`-(1)/(f)=(1)/(v)-(1)/(u)`

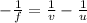
Solving for v,

`v=(1)/(-(1)/(f)+(1)/(u))`

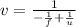
Substitute the known values and solve,

`v=(1)/(-(1)/(42.5)+(1)/(20))\approx37.78cm`

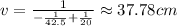
The magnification formula is,

`m=-(v)/(u)=-(37.78cm)/(-20cm)\approx1.89`

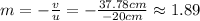
Hence, the magnification of the image is 1.89. As expected, it is a positive value because the image is upright.