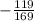Question

Given sine of x equals negative 12 over 13 and cos x > 0, what is the exact solution of cos 2x?

Answer 1

Use the definition of sine to find the known sides of the unit circle right triangle.

`\sin x=(opposite)/(hypotenuse)=-(12)/(13)`

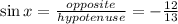
Find the adjacent side of the unit circle triangle. Since the hypotenuse and opposite sides are known, use the Pythagorean theorem to find the remaining side.

`\text{Adjacent =}\sqrt[]{hypotenuse^2-opposite^2}`

Replace the known values in the equation.

`Adjacent=\sqrt[]{13^2-(-12)^2}=\sqrt[]{169-144}=\sqrt[]{25}=5`

Find the value of cosine.

`\begin{gathered} \cos x=(adjacent)/(hypotenuse) \\ \cos x=(5)/(13) \end{gathered}`

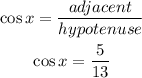
Next, we have

`\cos 2x=\cos ^2x-\sin ^2x`

Then, replace the values of sin(x) and cos(x)

`\cos 2x=((5)/(13))^2-(-(12)/(13))^2=(25)/(169)-(144)/(169)=(25-144)/(169)=-(119)/(169)`

Answer:

`-(119)/(169)`