Question

A lifeguard in a tower 20 ft above sea level spots a struggling surfer at an angle of depression of 15 degrees. How far is the surfer from the base of tower rounded to the nearest whole number? ft

Answer 1

The tower is 20 feet above the ground

and the angle of depression is 15 degree

Since Angle of Depression : Any angle form ny the horizontal line and a line to apoint below the line.

So, The figure will be:

We need to find the distance between the suffer and the base of the tower i.e. OB

The line AC is perpendicular to AO

so, angle CAO =90

then : angle CAO = angle BAO + angle BAC

90 = angle BAO + 15

Angle BAO = 90-15

Angle BAO = 75

Now apply the trignometric ratio of Tangent

`\tan \theta=(Perpendicular)/(Base)`

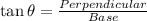
here we have angle is BAO

so,

`\begin{gathered} \tan \text{(}\angle\text{BAO)}=(Perpendicular)/(Base) \\ \text{tan(}\angle\text{BAO)}=(OB)/(OA) \\ OA(\tan \text{(}\angle\text{BAO))}=OB \\ 20(\tan 75)=OB \\ OB=20(\tan 75) \\ OB=20(3.73) \\ OB=74.6 \\ OB=75\text{ ft} \end{gathered}`

Answer :

The surfer from the base of tower is 75 ft away