13.2 m/s
Step-by-step explanation
Step 1
Diagram
the law of conservation of energy states that the total energy of an isolated system remains constant; it is said to be conserved over time. so, if we ignore the friction, we can se apply this to set an equation
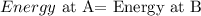
a) At a , the rollercoaster has
potential gravitational energy ( due to the heigth), as it start from the rest the velocity is zero,s o the kinetick energy is zero
b) at B, the rollercoster has
potential gravitational energy ( due to the heigth) and kinetick energy ( due to its mass ena velocity)
hence
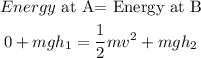
Step 2
let
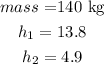
replace and solve for v
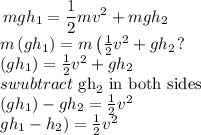
so
![\begin{gathered} 2*g\operatorname{\lparen}h_1-h_2)=v^2 \\ square\text{ root in both sides} \\ √(2g\lparen h_1-h_2))=\text{ v} \\ v=√(2*9.8\left(13.8-4.9\right?) \\ v=13.2\text{ m/s} \\ \\ \end{gathered}]()
therefore, the answer is
13.2 m/s
I hope this helps you