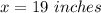Answer:
The smallest possible whole-number length of the unknown side is
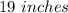
Explanation:
we know that
The triangle inequality theorem, states that the sum of the lengths of any two sides of a triangle is greater than the length of the third side
Let
x-----> the length of longest side
Applying the triangle inequality theorem
case A)


Rewrite
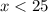
case B)
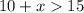
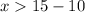
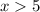
The solution of the third side is the interval------->
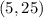
but remember that
In an obtuse triangle
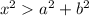
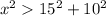
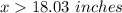
Round to a whole number