Question

If f(x)=x^2+3 and g(x)=1-xWhat is (fg)(4)=?

Answer 1

Given the functions:

`\begin{gathered} f(x)=x^2+3 \\ \\ g(x)=1-x \end{gathered}`

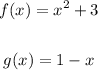
Let's find (fg)(4).

Let's first find (fg)(x):

`\begin{gathered} (fg)(x)=f(x)*g(x) \\ \\ (fg)(x)=(x^2+3)(1-x) \end{gathered}`

Expand the right side using FOIL method and distributive property:

`\begin{gathered} (fg)(x)=x^2(1-x)+3(1-x) \\ \\ (fg)(x)=x^2(1)+x^2(-x)+3(1)+3(-x) \\ \\ (fg)(x)=x^2-x^3+3-3x \\ \\ (fg)(x)=-x^3+x^2-3x+3 \end{gathered}`

Now, to find (fg)(4), substitute 4 for x in (fg)(x) and solve for (fg)(4):

`\begin{gathered} (fg)(4)=(-4)^3+(4)^2-3(4)+3 \\ \\ (fg)(4)=-64+16-12+3 \end{gathered}`

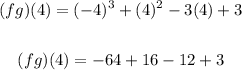
Solving further:

`(fg)(4)=-57`

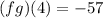
Therefore, the value of (fg)(4) is -57 .

ANSWER:

-57