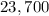Let
x-------> the number of x tires sold
y-------> the number of y tires sold
we know that
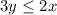 ------> equation
------> equation

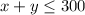 ------> equation
------> equation
using a graph tool
see the attached figure
the solution is the shaded area
the maximum revenue that the company can make is for the point
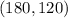

therefore
the answer is the option
$