Rearrange
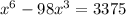
to give

Let
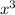
be a variable 'p' and so we can write
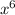
as

Rewrite the equation in terms of 'p'
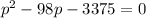
where

using the quadratic formula

and subsitute the value of
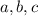

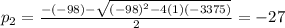
There are two value of p; 125 and -27
Now we find the value of x
Earlier we substitute
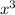
for
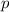
and
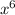
for
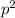
When
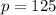
,
![x= \sqrt[3]{125}=5](https://img.qammunity.org/2018/formulas/mathematics/high-school/p3e4uag7raebvxbwdbnl110e4exzj3vq1q.png)
When
![p = -27, x= \sqrt[3]{-27}=-3](https://img.qammunity.org/2018/formulas/mathematics/college/i2q7ulfcja5tretxich1ehh43avejhw8pj.png)
So the final answer is the two values of x;
x = 5 OR x = -3