Question

-99.7%-95%68%The figure illustrates a normaldistribution for the prices paid for aparticular model of a new car. The meansis $19,000 and the standard deviation is$500.Use the 68-95-99.7 Rule to find thepercentage of buyers who paid between$17,500 and $19,000.Number of Car Buyers20.50017.500 18.000 18500 19.000 19.500 20.000Price of a Model of a New CarWhat percentage of buyers paid between $17,500 and $19,000?%

Answer 1

The 68-95-99.7 rule states that:

• 68% of the data is expected to be within one standard deviation from the mean.

• 95% of the data is expected to be within two standard deviations from the mean.

• 99.7% of the data is expected to be within three standard deviations from the mean.

Then, when the mean is $19,000 and the standard deviation is $500, we can estimate how many standard deviations we are from the mean for the values $17500 and $19000 calculating the z-score:

`\begin{gathered} z_1=(X_1-\mu)/(\sigma)=(17500-19000)/(500)=(-1500)/(500)=-3 \\ z_2=(X_2-\mu)/(\sigma)=(19000-19000)/(500)=(0)/(500)=0 \end{gathered}`

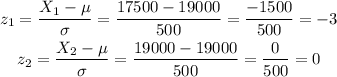
Then, we have three standard deviations to the left and no standard deviation from the mean for the right boundary.

We can picture this in the normal distribution curve as:

This is half the amount of data that if we have 3 standard deviations to each side of the mean, so we can expect to have 99.7% / 2 = 49.85% of the data within these limits.

Answer: 49.85%