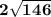we know that (-3,5) is the location of one of the endpoints.... and we know the midpoint is at (2,-6)... .now.. what's the distance between those two guys?
![\bf \textit{distance between 2 points}\\ \quad \\ \begin{array}{lllll} &x_1&y_1&x_2&y_2\\ % (a,b) &({{ -3}}\quad ,&{{ 5}})\quad % (c,d) &({{ 2}}\quad ,&{{ -6}}) \end{array}\qquad % distance value d = \sqrt{({{ x_2}}-{{ x_1}})^2 + ({{ y_2}}-{{ y_1}})^2} \\\\\\ d=√([2-(-3)]^2+[-6-5]^2)\implies d=√((2+3)^2+(-6-5)^2) \\\\\\ d=√(5^2+(-11)^2)\implies d=√(25+121)\implies d=√(146)]()
so, the distance "d" from the midpoint to that endpoint is that much. And the distance from the midpoint to the other endpoint is the same "d" distance, because the midpoint is half-way in between both endpoints.
so, the length of AB is twice that distance, or