Question

Integral (3,x) of sqrt ( 1+t^3) find (f^-1)'(0)

Answer 1

Assuming the problem as stated is, given


`f(x)=\displaystyle\int_3^x√(1+t^3)\,\mathrm dt`

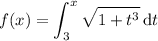
find
`(f^(-1))'(0)`.

Provided that
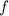
`f` is (at least locally) invertible, we have
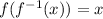
`f(f^(-1)(x))=x`, and differentiating both sides with respect to
`x` gives


`f'(f^(-1)(x))(f^(-1))'(x)=1\implies (f^(-1))'(x)=\frac1{f'(f^(-1)(x))}`

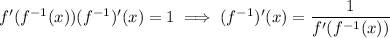
Notice that
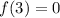
`f(3)=0`, which means
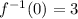
`f^(-1)(0)=3`. From this it follows that


`(f^(-1))'(0)=\frac1{f'(f^(-1)(0))}=\frac1{f'(3)}`

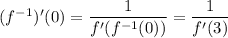
and since
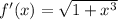
`f'(x)=√(1+x^3)` by the fundamental theorem of calculus, it follows that
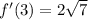
`f'(3)=2\sqrt7`, and so
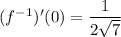
`(f^(-1))'(0)=\frac1{2\sqrt7}`.