Question

i need help A circle with radius 4 sits inside a circle with radius of 11 What is the area of the shaded region?

Answer 1

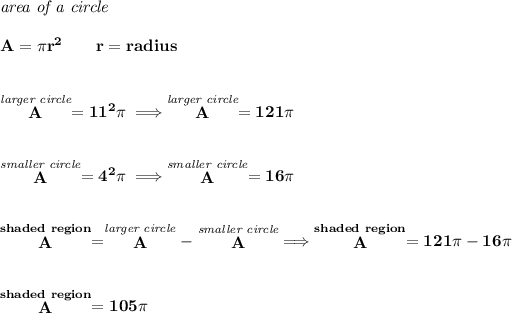
if you get the area of the larger circle containing the smaller one, its area includes the smaller's circle's area.

now, if you get the area of the smaller circle and subtract it from the area of the larger circle, you're in effect making a hole in the larger circle, and what's leftover, their difference, is the are not occupied by the smaller circle, since the smaller circle's area subtraction made a hole anyway.


`\bf \textit{area of a circle}\\\\ A=\pi r^2\qquad r=radius \\\\\\ \stackrel{\textit{larger circle}}{A}=11^2\pi \implies \stackrel{\textit{larger circle}}{A}=121\pi \\\\\\ \stackrel{\textit{smaller circle}}{A}=4^2\pi \implies \stackrel{\textit{smaller circle}}{A}=16\pi \\\\\\ \stackrel{shaded~region}{A}=\stackrel{\textit{larger circle}}{A}-\stackrel{\textit{smaller circle}}{A}\implies \stackrel{shaded~region}{A}=121\pi -16\pi \\\\\\ \stackrel{shaded~region}{A}=105\pi`

Answer 2

I'm guessing thet the shaded region is the outer ring.

This has area pi * 11^2 - pi * 4^2

= pi (121-16) = 105 pi or 330 to nearest whole number.