Question

consider the circle x^2+y^2-6x-8y=0. a.) find an equation of the tangent line to the circle at the point (0,0). b.) find the center and the radius of the circle (change into (x-a)^2+(y-b)^2=r^2 where (a,b) are the coordinates of the center and r is the radius. c.) find an equation of the tangent line to the circle at the point (6,0). d.) find the coordinates of the point where the two tangent lines intersect.

Answer 1

The slope of the tangent line of the circle
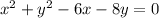
`x^2+y^2-6x-8y=0` is
`(dy)/(dx)`:

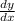
to find it we use implicit differentiation:


`(dy)/(dx)(x^2)+(dy)/(dx)(y^2)-(dy)/(dx)(6x)-(dy)/(dx)(8y)=0\\\\2x+2y \cdot(dy)/(dx)-6-8(dy)/(dx)=0\\\\(dy)/(dx)(2y-8)=-2x+6\\\\(dy)/(dx)= (-2x+6)/(2y-8)= (-x+3)/(y-4)`

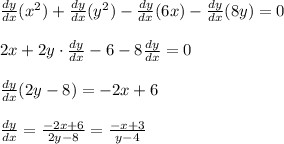
thus the slope of the tangent line at a point (x, y) of the circle is:


`m= (dy)/(dx)=(-x+3)/(y-4)`


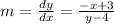
part a:

m at (0, 0) is (-0+3)/(0-4)=3/(-4)=-3/4

the equation of the tangent line is

(y-0)=(-3/4)(x-0)

y=(-3/4)x


part b)

The equation of the circle can be written in standard form by completing the square:


`x^2+y^2-6x-8y=0\\\\x^2-6x+y^2-8y=0\\\\(x^2-6x+9)-9+(y^2-8y+16)-16=0\\\\(x-3)^2+(y-4)^2=5^2`


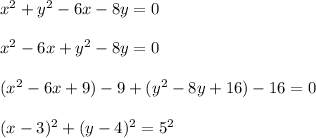
thus the circle has radius (3, 4) and radius 5.


part c.


`m=(-x+3)/(y-4)=(-6+3)/(0-4)= (-3)/(-4)= (3)/(4)`

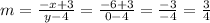
the equation of the line is:

y-0=(3/4)(x-6)

y=(3/4)x-9/2


d) the lines are y=(-3/4)x and y=(3/4)x-9/2

they meet at x:

(-3/4)x=(3/4)x-9/2

(-6/4)x=-9/2

(6/4)x=9/2

(2/2)x=3/1

x=3,

at x=3, y=(-3/4)x=(-3/4)*3=-9/4


Check the graph, generated using desmos.com