Question

A projectile is launched from a level surface toward a cliff. At launch, the projectile has a velocity of 276.62 m/s at an angle 44.78° above the horizontal. Air resistance is negligible. Calculate the horizontal distance that the projectile travels before it hits the ground.

Answer 1

We know that

• The initial velocity is 276.62 m/s.

,

• The angle of launch is 44.78.

The formula to find the horizontal distance reached is

`R=(v^2_0\sin 2\theta)/(g)`

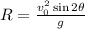
Using the given magnitudes, and g = 9.8 m/s^2, we have

`\begin{gathered} R=((276.62\cdot(m)/(s))^2\sin (2\cdot44.78))/(9.8\cdot(m)/(s^2)) \\ R=(76518.62\cdot(m^2)/(s^2)\cdot\sin (89.56))/(9.8\cdot(m)/(s^2)) \\ R\approx7807.8m \end{gathered}`

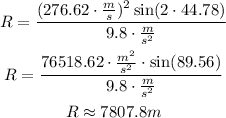
Therefore, the horizontal distance that the projectile travels before it hits the ground is 7807.8 meters.