We know that
• The initial velocity is 276.62 m/s.
,
• The angle of launch is 44.78.
The formula to find the horizontal distance reached is
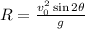
Using the given magnitudes, and g = 9.8 m/s^2, we have
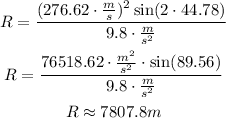
Therefore, the horizontal distance that the projectile travels before it hits the ground is 7807.8 meters.