Question

Which statement best describes how to determine whether f(x) = x3 + 5x + 1 is an even function?

Determine whether –(x3 + 5x + 1) is equivalent to x3 + 5x + 1.
Determine whether (–x)3 + 5(–x) + 1 is equivalent to x3 + 5x + 1.
Determine whether –x3 + 5x + 1 is equivalent to –(x3 + 5x + 1).
Determine whether (–x)3 + 5(–x) + 1 is equivalent to –(x3 + 5x + 1).

Answer 1

Its B -Determine whether (–x)3 + 5(–x) + 1 is equivalent to x3 + 5x + 1.

Answer 2

The right answer is: Determine whether
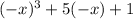`(-x)^3+5(-x)+1` is equivalent to
`x^3+5x+1`

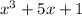
A function is said to be even if its graph is symmetric with respect to the
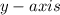`y-axis`. That is:

`A \ function \ y=f(x) \ is \ \mathbf{even} \ if, \ for \ each \ x \ in \ the \ domain \ of \  f:\\ \\ f(-x)=f(x)`

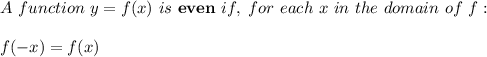
According to this definition, the statement that best describes if the function:

`f(x)=x^3+5x+1`

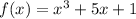
is even, is:

Determine whether
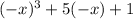`(-x)^3+5(-x)+1` is equivalent to
`x^3+5x+1`

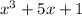
By doing this, we have:

`f(-x)=(-x)^3+5(-x)+1 \\ \\ \therefore \ f(-x)=-x^3-5x+1`

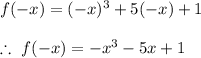
As you can see:

`f(x) \\eq f(-x)`

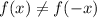
Conclusion: The function is not even.