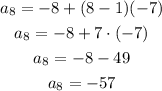Answer
-57
Explanation
Arithmetic sequence formula
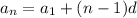
where
• aₙ is the ,nth, term
,
• a₁ is the first term
,
• n indicates the term position
,
• d is the common difference
Substituting a₁ = -8, n = 32, and the 32nd term = -225, and solving for d:
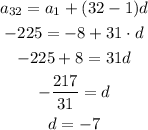
Substituting a₁ = -8, n = 8, d = -7, the value of the 8th term is: