Answer:
(a) y-(-5)= -3(x-1)
(b) y = -3x -2
Explanation:
Point slope form is
y-y1= m(x-x1)
Where m is the slope
slope formula is
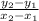
(x1,y1) is (1, –5) and (x2,y2) is (–3, 7)
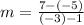
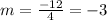
use m=-3 and point (1,-5)
y-y1= m(x-x1)
(a) Point - slope form is
y-(-5)= -3(x-1)
(b) Rewrite the equation in slope-intercept form, solve for y
y+5 = -3x + 3
Subtract 5 on both sides
y = -3x -2