a. gradient is also called the slope
take the derivative
use the chain and power rule
dy/dx=-12(1-2x)
at x=1
dy/dx=-12(1-2(1))
dy/dx=-12(1-2)
dy/dx=-12(-1)
dy/dx=12
the gradient is 12
b.
normal means the perpendicular line
the line perpendicular to that point has a slope that is a negative reciprocal of the slope of the line at that point
we found that the slope was 12 so the slope of the normal line would be the negative reciprocal of 12 or -1/12
use point-slope form
the equation of the line that has a slope of m and passes through (h,k) is
y-k=m(x-h)
we want the equation of the that has a slope of -1/12 and passes through (1,-2)
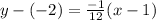
![y+2=(-1)/(12)(x-1)]](https://img.qammunity.org/2018/formulas/mathematics/middle-school/96prvnzmzjbjvrvw8cc4ym349jwpk6j7qu.png)
is the equation normal to the curve at (1,-2)