It is given that G lies in the interior of angle OMS.
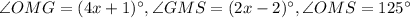
The diagram with the information is shown below:
From the figure it can be seen that the angle OMS is the sum of OMG and GMS so it follows:
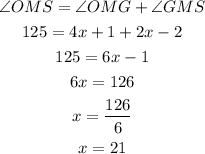
So the value of angle OMG is given by:
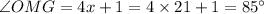
Hence angle OMG is 85 degrees.