From the definition of absolute value, we have the following:
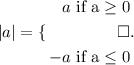
For this case we have:
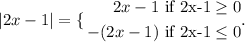
Therefore, we must solve for both cases. First, when 2x-1 is greater or equal to 0, we have:
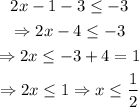
Now, for the second case we get:
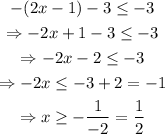
Notice how in this case we had to change the orientation of the sign since we divided by -2.
Since we have that x <= 1/2 and x>=1/2, then x=1/2