Answer:
Change in function f(x) to g(x): 5 unit up
Range: [2,8]
Explanation:
Given:
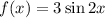
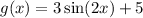
First we have to see the change from f(x) to g(x).
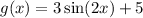
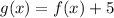
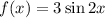
If we shift f(x) 5 unit up to get g(x)
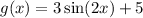
Effect: f(x) shift 5 unit up
Now we see change in range.
Range of
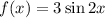
![[-3,3]](https://img.qammunity.org/2018/formulas/mathematics/college/gya55qlrjq0xei4len3hb7bxu748kta8zt.png)
Graph shift 5 unit up.
So, Range will shift 5 unit up.
Range of
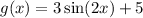
![[-3+5,3+5]\Rightarrow [2,8]](https://img.qammunity.org/2018/formulas/mathematics/college/9b5ffasbu0jyqujuw5s7omohbj9gja2sn8.png)
Hence, The range of g(x) is [2,6]