Question

Which table represents points in the graph of h(x)

Answer 1

hello :
the third table because ;
f(-6) = 2
f(1) =1
f(2) =0
f(3) =-1
f(6) =-2

Answer 2

The table in the attached figure

Explanation:

we have

`h(x)=\sqrt[3]{-x+2}`

Using a graphing tool

see the attached figure

The x-intercept of the function is the point
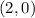`(2,0)` (value of x when the value of the function is equal to zero)

The y-intercept of the function is the point
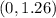`(0,1.26)` (value of the function when the value of x is equal to zero)

therefore

First table

The y-intercept of the function is the point
`(0,2)`

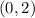
so

Is not represent the function h(x)

Second table

The y-intercept of the function is the point
`(0,2)`

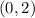
so

Is not represent the function h(x)

Third table

The x-intercept of the function is the point
`(2,0)`

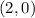
so

Could be represent the function h(x)

Fourth table

The x-intercept of the function is the point
`(-2,0)`

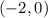
so

Is not represent the function h(x)

Verify the third table

For
`x=-6`

Find the value of y

substitute the value of x

`h(-6)=\sqrt[3]{-(-6)+2}=2` -----> is ok

For
`x=1`

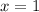
Find the value of y

substitute the value of x

`h(1)=\sqrt[3]{-(1)+2}=1` -----> is ok

For
`x=3`

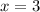
Find the value of y

substitute the value of x

`h(3)=\sqrt[3]{-(3)+2}=-1` -----> is ok

For
`x=10`

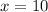
Find the value of y

substitute the value of x

`h(10)=\sqrt[3]{-(10)+2}=-2` -----> is ok

The third table represent the function h(x) ------> see the attached figure