Given the set of vectors {u, v, w}:
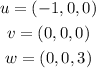
This set is said to be linearly independent if there is a non-trivial solution to the equation:
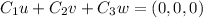
Where C₁, C₂, and C₃ are real constants. In this case, we see that if C₁ and C₃ are 0, we will have:
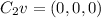
But v is already the null vector (0, 0, 0), so it doesn't matter the value of C₂ this equation will always be true. Then, we found a non-trivial solution, hence the system is linearly dependent.
If it is linearly dependent, it can not be used to span R³