Given;
sample, n = 8 people
sample mean, x' = 34.5 min
sample standard deviation, s = 7.3 min
90% confidence interval, CI = (29.6,39.4)
population standard deviation is 8.9 min
Find;
Margin of error, M
90% confidence interval using the standard normal distribution with the appropriate calculations for a standard deviation that is known.
Margin of error formula:
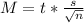
t is the critical value for a 2 tailed test at a 10% level of significance
degree of freedom = sample size - 1, df = 8 - 1 = 7
and the level of significance α = 10%
The value of t from a t distribution table is; t = 1.8946
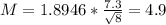
Another way to calculate M, is by substracting CI - x' = 39.4 - 34.5 = 4.9
Now, let's construct the 90% CI using s = 8.9
The new Margin of error, M* is:
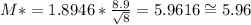
Therefore, the new Confidence interval, CI* is
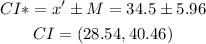
Answer: New margin of error, M* = 5.96, New confidence interval, CI* = (28.54,40.46)
comparison:
Initial margin of error, M = 4.9
New margin of error, M* = 5.96
Initial confidence interval, CI = (29.6,39.4)
New confidence interval, CI* = (28.54,40.46)