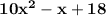Answer:
The perimeter of triangle is:
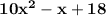
Explanation:
We need to find perimeter, in terms of x, of the triangle shown here.
The length of side 1:
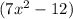
The length of side 2:
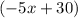
The length of side 3:
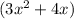
The formula used to find perimeter of triangle is:
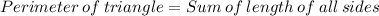
Putting values and finding perimeter:
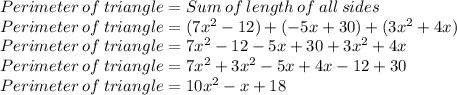
So, The perimeter of triangle is: