Answer:
The correct answer is:
Option A. a_n=9+(n-1)(-3)
Explanation:
Given that
a1 = 9
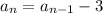
We can see that in recursive formula the next term is being obtained by subtracting 3 from previous term
That means that the common difference is -3
We also know the first term
The general form of explicit formula for an arithmetic sequence is:
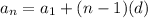
We know that a1 = 9 and d = -3
Putting the values we get
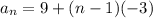
Hence the correct answer is:
Option A. a_n=9+(n-1)(-3)