Question

An arithmetic sequence has this recursive formula:

a1=9
an=an-1 -3
What is the explicit formula for this sequence?
A. an=9+(n-1)(-3)
B. an=-3+(n-1)9
C. an=9+(n-3)(-1)
D. an=-1+(n-9)(-3)

Answer 1

The correct answer is:

Option A. a_n=9+(n-1)(-3)

Explanation:

Given that

a1 = 9

`a_n = a_(n-1)-3`

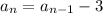
We can see that in recursive formula the next term is being obtained by subtracting 3 from previous term

That means that the common difference is -3

We also know the first term

The general form of explicit formula for an arithmetic sequence is:

`a_n = a_1 + (n-1)(d)`

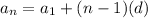
We know that a1 = 9 and d = -3

Putting the values we get

`a_n = 9+(n-1)(-3)`

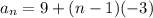
Hence the correct answer is:

Option A. a_n=9+(n-1)(-3)